Les arbres en informatique

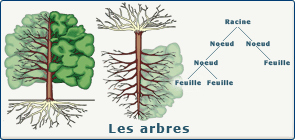
Dans notre drôle de monde informatique, les arbres poussent à l'envers. En effet, nous considérons que la racine de l'arbre se trouve généralement en haut. Nous jouons au jardinier fou en modifiant la forme de l'arbre ou en déplaçant tous ses fruits. Nous passons notre temps à peinturlurer en rouge ou en noir les endroits où les branches prennent naissance, et comme des singes acrobates nous passons notre temps à essayer de parcourir l'arbre de différentes manières.

Définition d'un arbre

Un arbre est une structure de données. Comme pour un arbre naturel, nous distionguons un certain nombre d'éléments constituants :

nœud : le nœud est le point de départ d'une ou de plusieurs branches. Nous pouvons utiliser la terminologie de la généalogie pour désigner les relations qu'il existe entre les nœuds : le parent, le grand-parent, les enfants, le fils, le frère (nœud de même niveau et de même parent), l'oncle (le frère du parent), le cousin (nœud de même niveau mais de parent différent), etc.
racine : la racine est un nœud particulier car il ne possède pas de nœud parent.
feuille : une feuille est un nœud particulier car il ne possède pas d'enfant.

Selon la théorie des graphes, un arbre est un graphe (généralement non orienté car nous n'avons pas de pointeur vers le parent) qui possède uneseule racine (sommet de degré nul)¹, et n'admet pas de cycle.

En plus de ces termes, nous aurons à utiliser différentes notions relatives aux arbres :

arête : si nous considérons l'arbre comme un graphe non orienté, nous préférerons employer le terme arête à la place de branche pour désigner le segment de droite qui relie deux nœuds.
profondeur d'un nœud : c'est la distance d'un nœud par rapport à la racine (la racine + le nombre de nœuds entre la racine et le nœud + le nœud lui même).
hauteur de l'arbre : c'est la profondeur de la feuille la plus basse, ou encore la plus grande profondeur parmi toutes les feuilles.
taille de l'arbre : c'est le nombre total de nœuds présents dans l'arbre. Selon les cas, nous pouvons préciser qu'il s'agit d'une taille de l'arbre sans la racine ou sans les feuilles.

Jusqu'à présent, nous ne nous sommes préoccupés que de la structure de l'arbre, mais il est intéressant de pouvoir y placer certaines informations (il est temps que l'arbre porte ses fruits). Nous pouvons utiliser chaque nœud pour y placer de l'information. Si ces informations possèdent une manière de les comparer, la structure de l'arbre se prête assez bien à ce genre de besoin, comme nous le verrons plus tard.

Comme l'informatique est par essence dichotomique car basée sur la dualité 0-1 du binaire, nous pouvons nous pencher sur certains arbres particulier, les arbres binaires, car ils sont les plus faciles à implémenter. Nous ne devons cependant pas oublier que la définition même de la structure en arbre admet plus de deux enfants pour chaque nœud, et nous serons amenésà utiliser aussi ce genre d'arbre.

Structure générale d'un arbre binaire

Afin de répondre aux différents besoins, nous avons besoin de trois éléments :

un moyen d'atteindre le fils de gauche
la donnée utile, ou un moyen d'atteindre cette donnée
un moyen d'atteindre le fils de droite

Parcourir un arbre binaire

Pour chaque nœud (y compris la racine), trois possibilités s'offrent à nous :

Nous nous dirigeons vers la branche de gauche si elle existe (G).
Nous nous dirigeons vers la branche de droite si elle existe (D).
Nous traitons la valeur courante (T).

Nous pouvons combiner ces actions de différentes manières, et nous devons considérer la position du traitement de la valeur courante (T).
Ce traitement peut se faire à trois moments :

Avant toute décision de direction (ex: TGD). Nous parlerons de traitement préfixe.
Après la première décision (ex: GTD). Nous parlerons de traitement infixe.
Après toute décision de direction (ex: GDT). Nous parlerons de traitement postfixe.

English translation

You have asked to visit this site in English. For now, only the interface is translated, but not all the content yet.

If you want to help me in translations, your contribution is welcome. All you need to do is register on the site, and send me a message asking me to add you to the group of translators, which will give you the opportunity to translate the pages you want. A link at the bottom of each translated page indicates that you are the translator, and has a link to your profile.

Thank you in advance.

Document created the 02/11/2009, last modified the 26/10/2018
Source of the printed document:https://www.gaudry.be/en/programmer-arbres.html

The infobrol is a personal site whose content is my sole responsibility. The text is available under CreativeCommons license (BY-NC-SA). More info on the terms of use and the author.

Notes

↑ Racine : Certaines définitions de l'arbre au sens informatique différencient les arbres les arbres enracinés (qui possèdent une racine) des arbres non enracinés (qui ne possèdent pas de racine). Sans rentrer dans le débat de l'utilité d'un arbre non enraciné et de la pertinence de sa définition, je n'utiliserais le terme arbre que pour désigner des arbres enracinés.

Contents Haut

References

These references and links indicate documents consulted during the writing of this page, or which may provide additional information, but the authors of these sources can not be held responsible for the content of this page.
The author This site is solely responsible for the way in which the various concepts, and the freedoms that are taken with the reference works, are presented here. Remember that you must cross multiple source information to reduce the risk of errors.

Contents Haut