Graphes et arbres
Arbre
Un arbre est un graphe simplement connexe, non orienté, sans cycles (et donc forcément sans boucles1), dans lequel nous ne pouvons retrouver qu'une seule chaîne pour relier deux sommets distincts.
Le graphe d'un arbre comporte toujours exactement n-1 arêtes2.
Racine d'un graphe
La racine r dans le cas d'un graphe orienté est le sommet à partir duquel nous pouvons accéder à chaque autre sommet du graphe : ∀ y : M[r,y]=1. Ce sommet (racine) est dit ascendant à tout autre sommet.
Arborescence
Nous appelons arborescence un graphe orienté qui possède une racine et pour lequel nous avons pour chaque sommet un seul chemin depuis la racine.
Arbre et arborescence
Les concepts d'arbre et d'arborescence ne sont pas figés. Dans certains cas nous aurons besoin de passer d'une notion à l'autre.
Nous pouvons orienter un arbre à partir d'un sommet. Dans ce cas nous pouvons avoir une arborescence.
Nous pouvons considérer une arborescence comme un graphe non orienté, et dans ce cas nous avons un arbre.
Lorsque nous ne pouvons ajouter une arête ou un arc d'un graphe à un de ses sous-graphes sans perdre le caractère d'arbre ou d'arborescence, nous pouvons dire que le sous-graphe est un arbre maximal ou une arborescence maximale.
Forêt
Lorsque nous avons un graphe composé d'arbres, nous parlons de forêt. Comme un arbre peut généralement être décomposé en sous-arbres, nous avons généralement une forêt dès que nous avons un arbre dans notre graphe.
Exercice
Voici quelques graphes, à vous de déterminer si nous sommes en présence d'un arbre, d'une arborescence, d'une forêt...
| 
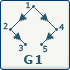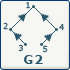| L'orientation de G2 ne nous permet pas de déterminer une racine.
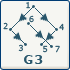| Par contre nous avons 2 arbres constituées par les sous graphes {1,2,3,4,5} et {6,7}
Par contre nous avons 2 arborescences constituées par les sous graphes {1,2,3,4,5} et {6,7}
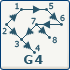| Nous sommes en présence d'un cycle.
Il existe par exemple plusieurs chemins depuis 2 vers 3
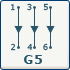| Par contre nous avons 3 arbres constituées par les sous graphes {1,2}, {3,4} et {5,6}
Par contre nous avons 3 arborescences constituées par les sous graphes {1,2}, {3,4} et {5,6}
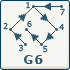| L'orientation de G6 ne nous permet pas de déterminer une racine.
English translation
You have asked to visit this site in English. For now, only the interface is translated, but not all the content yet.If you want to help me in translations, your contribution is welcome. All you need to do is register on the site, and send me a message asking me to add you to the group of translators, which will give you the opportunity to translate the pages you want. A link at the bottom of each translated page indicates that you are the translator, and has a link to your profile.
Thank you in advance.
Document created the 22/11/2009, last modified the 09/03/2020
Source of the printed document:https://www.gaudry.be/en/graphes-arbres.html
The infobrol is a personal site whose content is my sole responsibility. The text is available under CreativeCommons license (BY-NC-SA). More info on the terms of use and the author.
References
Arbres : lien interne, Les arbres en programmation.
INFOB321 - Théorie des graphes : JP Leclercq, Cours de Théorie des Graphes et réseaux de Petri
(September 2008)
These references and links indicate documents consulted during the writing of this page, or which may provide additional information, but the authors of these sources can not be held responsible for the content of this page.
The author This site is solely responsible for the way in which the various concepts, and the freedoms that are taken with the reference works, are presented here. Remember that you must cross multiple source information to reduce the risk of errors.
