Opérations sur les matrices
Egalité de matrices
Définition
Deux matrices A = (aij) et B = (bij) sont égales si
- elles sont de même format.
- aij = bij pour tout i et j.
Somme de deux matrices
Définition
Soit deux matrices A = (aij) et B = (bij), la somme des deux matrices est une matrice C = (cij)
- de même format.
- telle que cij = aij + bij pour tout i et j.
Exemple
Soit A et B les matrices suivantes :
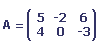
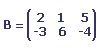
La somme des deux matrices est la matrice suivante :
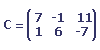
Remarque: l'addition est commutative (A+B=B+A).
Différence de deux matrices
Définition
Soit deux matrices A = (aij) et B = (bij), la différence des deux matrices est une matrice C = (cij)
- de même format.
- telle que cij = aij - bij pour tout i et j.
Exemple
Soit A et B les matrices suivantes :
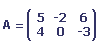
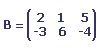
La différence des deux matrices est la matrice suivante :
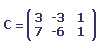
Remarques :
- La différence n'est pas commutative.
- A-B = -(B-A).
Produit d'une matrice par un scalaire
Définition
Soit une matrice quelconque A = (aij), et un scalaire ß, le produit des deux est une matrice B = (bij)
- de même format que A.
- telle que bij = ßaij pour tout i et j.
Exemple
Soit A la matrice suivantes:

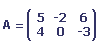
Le produit de la matrices et du scalaire 2 est la matrice suivante:

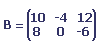
Produit de deux matrices
Définition
Soit deux matrices A = (aij) de format m*n, et B = (bij) de format n*p,
le produit des deux matrices est une matrice C = (cij)
- de format m*p.
- telle que cij est le produit de la ligne i de A par la colonne j de B pour tout i et j.
Exemple
Soit A et B les matrices suivantes:
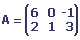
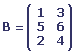
Le produit des deux matrices est la matrice suivante:
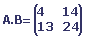
Remarque:
- Le produit matriciel n'est pas commutatif.
Nederlandse vertaling
U hebt gevraagd om deze site in het Nederlands te bezoeken. Voor nu wordt alleen de interface vertaald, maar nog niet alle inhoud.Als je me wilt helpen met vertalingen, is je bijdrage welkom. Het enige dat u hoeft te doen, is u op de site registreren en mij een bericht sturen waarin u wordt gevraagd om u toe te voegen aan de groep vertalers, zodat u de gewenste pagina's kunt vertalen. Een link onderaan elke vertaalde pagina geeft aan dat u de vertaler bent en heeft een link naar uw profiel.
Bij voorbaat dank.
Document heeft de 19/03/2002 gemaakt, de laatste keer de 26/10/2018 gewijzigd
Bron van het afgedrukte document:https://www.gaudry.be/nl/matrices-operations.html
De infobrol is een persoonlijke site waarvan de inhoud uitsluitend mijn verantwoordelijkheid is. De tekst is beschikbaar onder CreativeCommons-licentie (BY-NC-SA). Meer info op de gebruiksvoorwaarden en de auteur.


