Méthode de Karnaugh
Introduction
La méthode de Karnaugh permet la simplification de l'écriture des fonctions logiques.
Cette méthode est basée sur la mise en évidence: A . B + A . B = A . (B + B) = A (car B + B = 1).
Un tableaux de Karnaugh est une représentation bidimensionnelle (lignes et colonnes) d'une table de vérité (ligne par ligne). Chaque cellule du tableau doit correspondre à une ligne de la table de vérité.
- Pour 2 variables, nous obtenons 4 cas possibles répartis sur 2 lignes et 2 colonnes.
- Pour 3 variables, nous obtenons 8 cas possibles répartis sur 2 lignes et 4 colonnes.
- Pour 4 variables, nous obtenons 16 cas possibles répartis sur 4 lignes et 4 colonnes.
Nous nous limiterons à 4 variables dans les exemples et démonstrations.
Si une fonction dépend de n variables il y a 2n produits possibles. Chacun de ces produits est représenté par une case dans un tableau. Les figures suivantes donnent la structure des tableaux de Karnaugh pour 2 et 4 variables.
Tableau à 2 variables
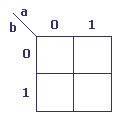
Tableau à 4 variables
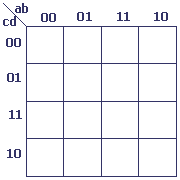
Nous devons remarquer ici la méthode d'adressage des cellules, qui ne suit pas une logique binaire (00, 01, 10, 11), mais bien le code Gray (00, 01, 11, 10): pour chaque étape, un seul des deux bits peut subir un changement d'état.
Représentation des variables
Voyons maintenant comment représenter des variables sur les tableaux. Il suffit de regarder les valeurs de vérité qui adressent les cellules. Par exemple, représentons la fonction a . ¬b:
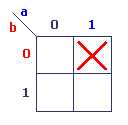
La valeur de a est vrai (1), et la valeur de b est faux (0). Ce n'est pas plus compliqué que cela.
Valeurs des cellules
Tableau à 2 variables
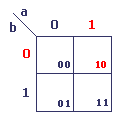
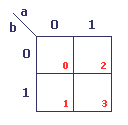
La valeur des cellules est le résultat de leur adressage. Il est possible ensuite de convertir ces valeurs hexadécimales en valeurs décimales, ce qui permettra ultérieurement de représenter une fonction logique par la somme des adresses des cellules.
L'adressage de la cellule en rouge dans notre exemple se fait de la manière suivante: La valeur de a est vrai (1), et la valeur de b est faux (0).
Nous devons ensuite convertir cette valeur hexadécimale en valeur décimale, ce qui nous donne la valeur 2.
Tableau à 4 variables
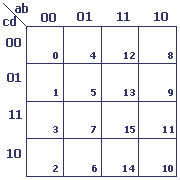
Le procédé est identique pour les tableaux à 3, 4, et 5 variables.
Remarque:
Il ne faut cependant pas perdre de vue que la méthode d'adressage suit le code Gray.
Les boucles
Reprenons notre exemple de tableau à 4 variables:
Afin de simplifier les fonctions logiques, il nous faudra sélectionner un maximum de cellules juxtaposées, afin de former un minimum de "boucles" les plus larges possibles, sans oublier de sélectionner au moins une fois chaque cellule.
« Mais keskidit? »
Bon, je résume:
- Chaque cellule qui est adressée doit être sélectionnée.
- Une cellule peut appartenir à plusieurs boucles (car A + A = A).
- Boucle (ou bloc): ensemble de 2n cellules disposées en carré ou en rectangle, correspondant à une variable, ou à un produit de variables.
- Nous devons faire un minimum de boucles.
- Les boucles doivent être les plus larges possibles:
- Boucle de 1 cellule = produit de 4 variables (=> minterm => cas spécial de monôme).
- Boucle de 2 cellules = produit de 3 variables (=> monôme).
- Boucle de 4 cellules = produit de 2 variables (=> monôme).
- Boucle de 8 cellules = une seule variable.
- Boucle de toutes les cellules = aucune variable (tautologie).
"Effet cylindre"
Les boucles délimitent des ensembles de cellules jointes, mais il est nécessaire de prendre en compte un aspect du tableau que nous pouvons appeler l'effet de cylindre. Les bords opposés du tableau sont joints deux à deux, ce qui permet de dire que le tableau est à la fois un cylindre horizontal, et un cylindre vertical.
Exemples :
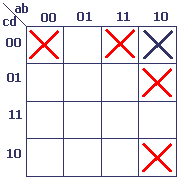
La cellule désignée par une croix sombre (1000 ou 8 en décimal) est jointive par les cellules marquées d'une croix rouge. Nous pouvons remarquer que la cellule 0000 est jointe à cette dernière par un effet de cylindre vertical. Un effet de cylindre horizontal joint la cellule 1010 à la cellule 1000.
Je tiens à vous faire remarquer ici que nous sommes face à une source d'erreur fréquente: Il arrive très souvent que l'on ne remarque pas la possibilité de créer des boucles en joignant les côtés opposés, et le résultat de la simplification est incorrect.
Karnaugh, exemples de simplifications
a . ¬b + ¬a . b
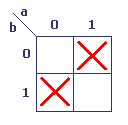
Il n'est pas possible de simplifier l'expression, car les cellules ne sont pas jointives.
Sous forme décimale, nous obtenons R = å 2, 1. Le résultat est la somme des cellules 2 et 1.
R = å 2, 3

Après avoir converti les valeurs hexadécimales des cellules en valeurs décimales, nous trouvons les cellules à marquer (du chiffre 1 pour vrai, ou comme ici par une croix).
L'expression algébrique est donc R = a . b + a . b
Simplification algébrique: a . b + a . b = a . (b + b) = a (car b + b = 1 et a + 1 = a).
Etant donné que les deux cellules sont jointives, nous pouvons nous dire que la variable b n'influence pas le résultat (que b soit égal à 0 ou à 1 ne change rien). Si une variable n'influence pas le résultat, nous pouvons l'éliminer.
La réponse est mise de suite en évidence par la boucle en rouge qui correspond à la variable a.
Exemples de boucles
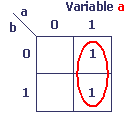
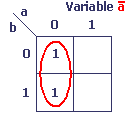
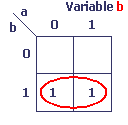
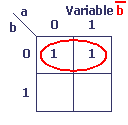
Nederlandse vertaling
U hebt gevraagd om deze site in het Nederlands te bezoeken. Voor nu wordt alleen de interface vertaald, maar nog niet alle inhoud.Als je me wilt helpen met vertalingen, is je bijdrage welkom. Het enige dat u hoeft te doen, is u op de site registreren en mij een bericht sturen waarin u wordt gevraagd om u toe te voegen aan de groep vertalers, zodat u de gewenste pagina's kunt vertalen. Een link onderaan elke vertaalde pagina geeft aan dat u de vertaler bent en heeft een link naar uw profiel.
Bij voorbaat dank.
Document heeft de 19/03/2002 gemaakt, de laatste keer de 07/04/2023 gewijzigd
Bron van het afgedrukte document:https://www.gaudry.be/nl/logique-karnaugh.html
De infobrol is een persoonlijke site waarvan de inhoud uitsluitend mijn verantwoordelijkheid is. De tekst is beschikbaar onder CreativeCommons-licentie (BY-NC-SA). Meer info op de gebruiksvoorwaarden en de auteur.




