Demi additionneur binaire (half-adder)
Introduction
L'addition et la soustraction sont deux opérations arithmétiques de base. Nous allons donc tenter de comprendre comment l'ordinateur peut effectuer une addition.
En base 2, l'addition de deux bits correspond à ceci:
- 0 + 0 = 00
- 0 + 1 = 01
- 1 + 0 = 01
- 1 + 1 = 10
Décomposition du principe d'addition
Nous pouvons comparer cette addition avec une addition décimale, dans la mesure où il est possible d'avoir un report; rappelons nous l'addition des chiffres 5 et 6 en calcul écrit en base 10:
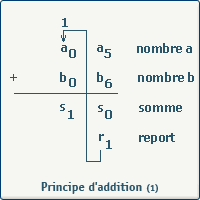
A partir du moment où un report intervient, nous devons envisager qu'il existe pour toute addition un report en entrée, et un report en sortie.
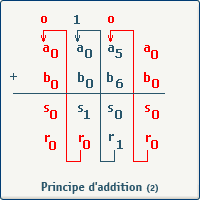
Le premier et le dernier report (en rouge dans le schéma) ont donc la valeur zéro. Il nous suffira donc d'initialiser le premier report à zéro; et le dernier report nous indiquera, dans le cas où il sera différent de zéro, qu'il y a dépassement de capacité (overflow).
Ceci nous permet de découper une addition complexe en une séquence utilisant à chaque fois le même traitement, ce que nous détaillerons dans la partie électronique.
L'addition des deux bits de bas poids (LSB: Least Significant Bit) a0 et b0, donne un résultat partiel s0 et une retenue r0. On forme ensuite la somme des deux bits a1 et b1 et de la retenue r0. Nous obtenons un résultat partiel s1 et une retenue r1. Et ainsi de suite, nous obtenons un résultat sur quatre bits S et une retenue r3.
Principe d'addition binaire: résumé
La figure suivante montre la décomposition de l'addition de deux nombres binaires de quatre bits.
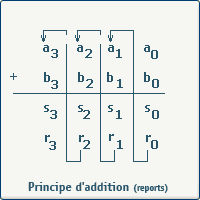
Schéma et table de vérité
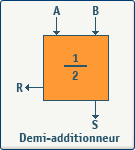
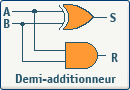
En entrée, nous avons les deux nombres à additionner (A et B), et en sortie, La somme (S) et le report (R). Ce module se nomme demi additionneur (half-adder), et nous pouvons constater qu'il ne tient pas compte du report d'entrée. Voyons donc la table de vérité :
Nous pouvons tirer certaines conclusions de cette table de vérité:
- S = A . B + A . B= A Å B
- R = A . B
Circuit logique du demi additionneur
Nederlandse vertaling
U hebt gevraagd om deze site in het Nederlands te bezoeken. Voor nu wordt alleen de interface vertaald, maar nog niet alle inhoud.Als je me wilt helpen met vertalingen, is je bijdrage welkom. Het enige dat u hoeft te doen, is u op de site registreren en mij een bericht sturen waarin u wordt gevraagd om u toe te voegen aan de groep vertalers, zodat u de gewenste pagina's kunt vertalen. Een link onderaan elke vertaalde pagina geeft aan dat u de vertaler bent en heeft een link naar uw profiel.
Bij voorbaat dank.
Document heeft de 19/03/2002 gemaakt, de laatste keer de 26/10/2018 gewijzigd
Bron van het afgedrukte document:https://www.gaudry.be/nl/logique-half-adder.html
De infobrol is een persoonlijke site waarvan de inhoud uitsluitend mijn verantwoordelijkheid is. De tekst is beschikbaar onder CreativeCommons-licentie (BY-NC-SA). Meer info op de gebruiksvoorwaarden en de auteur.
Referenties
Deze verwijzingen en links verwijzen naar documenten die geraadpleegd zijn tijdens het schrijven van deze pagina, of die aanvullende informatie kunnen geven, maar de auteurs van deze bronnen kunnen niet verantwoordelijk worden gehouden voor de inhoud van deze pagina.
De auteur van deze site is als enige verantwoordelijk voor de manier waarop de verschillende concepten, en de vrijheden die met de referentiewerken worden genomen, hier worden gepresenteerd. Vergeet niet dat u meerdere broninformatie moet doorgeven om het risico op fouten te verkleinen.



