Graphes : matrice d'adjacence

Introduction

Nous utiliserons dans les exemples la notation définie lors de l'introduction aux graphes.

Principe de la matrice d'adjacence

$Graphes: matrice d'adjacence$

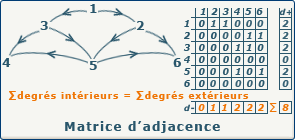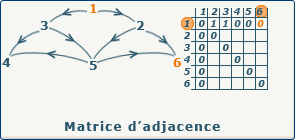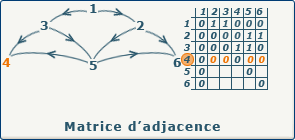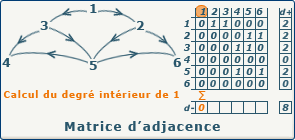
Nous pouvons représenter notre graphe G(X,A) sous la forme d'une matrice carrée de taille n*n. La ligne correspond au sommet de départ, et la colonne au sommet d'arrivée.

Ensuite, nous pouvons placer dans chaque case de notre matrice la valeur 0 ou 1 selon que le couple formé par l'indice de ligne et l'indice de colonne corresponde ou pas à un ensemble de A (en clair, 1 si l'arc existe dans le graphe). Ceci peut se traduire par la formule suivante : A_ij = 0 si (x_i,x_j)∉A, 1 si (x_i,x_j)∈A

Dans le cas d'un graphe non-orienté, notre matrice d'adjacence sera donc symétrique (x_ij=x_ji).

Nous pouvons trouver au maximum n! matrices d'adjacence pour notre graphe, selon l'ordre dans lequel nous considérons les sommets.

Algorithme de la matrice d'adjacence

Soient les matrices M, A, et B implémentées sous formes de tableaux de tableaux :

pour i variant_de 1 jusque n faire
	pour j variant_de 1 jusque n faire
		M[i,j] := 0;
		pour k variant_de 1 jusque n faire
			M[i,j] := M[i,j] &oplus; A[i,k] &otimes; B[k,j];
		fin pour
	fin pour
fin pour

Ce genre d'algorithme effectue le plus souvent le plus souvent le calcul suivant 0*0. Les deux boucles extérieures sont indispensables, mais nous pouvons par contre remplacer la boucle intérieure par les pointeurs d'arcs si ces derniers sont disponibles.

Inhoudsopgave Haut

Matrice de poids des arcs

$Matrice de poids des arcs$

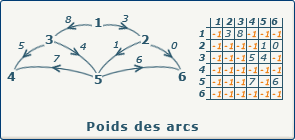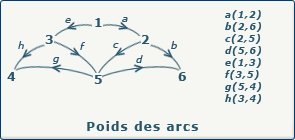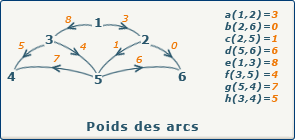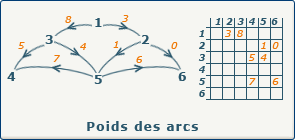
Si nous travaillons avec un graphe valué, au lieu de placer la valeur 1 quand un arc est présent, nous allons placer le poids (la valeur) de cet arc dans la case appropriée de la matrice.

Attention que dans ce cas, nous ne pouvons plus placer la valeur 0 pour signaler un arc inexistant, car cela représenterait un arc existant, de poids 0. Nous allons donc choisir arbitrairement une valeur non utilisée (par exemple -1 si nous avons la certitude que toutes nos valeurs sont positives).

Nederlandse vertaling

U hebt gevraagd om deze site in het Nederlands te bezoeken. Voor nu wordt alleen de interface vertaald, maar nog niet alle inhoud.

Als je me wilt helpen met vertalingen, is je bijdrage welkom. Het enige dat u hoeft te doen, is u op de site registreren en mij een bericht sturen waarin u wordt gevraagd om u toe te voegen aan de groep vertalers, zodat u de gewenste pagina's kunt vertalen. Een link onderaan elke vertaalde pagina geeft aan dat u de vertaler bent en heeft een link naar uw profiel.

Bij voorbaat dank.

Document heeft de 11/11/2009 gemaakt, de laatste keer de 26/10/2018 gewijzigd
Bron van het afgedrukte document:https://www.gaudry.be/nl/graphes-matrice-adjacence.html

De infobrol is een persoonlijke site waarvan de inhoud uitsluitend mijn verantwoordelijkheid is. De tekst is beschikbaar onder CreativeCommons-licentie (BY-NC-SA). Meer info op de gebruiksvoorwaarden en de auteur.

Referenties

INFOB321 - Théorie des graphes : JP Leclercq, Cours de Théorie des Graphes et réseaux de Petri (September 2008)

Deze verwijzingen en links verwijzen naar documenten die geraadpleegd zijn tijdens het schrijven van deze pagina, of die aanvullende informatie kunnen geven, maar de auteurs van deze bronnen kunnen niet verantwoordelijk worden gehouden voor de inhoud van deze pagina.
De auteur Deze site is als enige verantwoordelijk voor de manier waarop de verschillende concepten, en de vrijheden die met de referentiewerken worden genomen, hier worden gepresenteerd. Vergeet niet dat u meerdere broninformatie moet doorgeven om het risico op fouten te verkleinen.

Inhoudsopgave Haut