Matrices particulières
Matrice carrée
Une matrice est appelée carrée lorsque les nombres de lignes et de colonnes sont identiques.
Exemple:
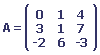
La matrice A possède trois lignes et trois colonnes, elle est donc carrée.
Vecteur ligne
Un vecteur ligne est une matrice qui possède une seule ligne.
Exemple:
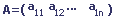
Vecteur colonne
Un vecteur colonne est une matrice qui possède une seule colonne.
Exemple:
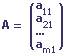
Matrice scalaire
Une matrice scalaire est une matrice qui ne possède qu'une seule ligne et une seule colonne (elle ne possède donc qu'un seul élément).
Exemple:
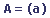
Matrice diagonale
Une matrice diagonale est une matrice carrée dont tous les éléments non compris dans la diagonale principale sont nuls.
Exemples:
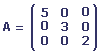 ou
ou 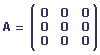
Matrice identité
Une matrice identité (ou unité) est une matrice diagonale dont les éléments de la diagonale principale sont de valeur 1.
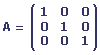
Matrice triangulaire
Une matrice triangulaire est une matrice carrée dont les éléments d'un même côté de la diagonale principale sont de valeur 0.
Matrice triangulaire supérieure
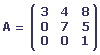
Matrice triangulaire inférieure
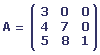
Transposée d'une matrice
Nous obtenons la transposée d'une matrice en permutant les lignes et les colonnes:
Remarques:
- La transposée de la matrice A se note donc tA.
- La transposée de la matrice de format m*n est une matrice de format n*m.
- Si tA=A, nous pouvons dire que la matrice est symétrique (elle doit donc être carrée).
- Si tA=-A, nous pouvons dire que la matrice est antisymétrique.
Version en cache
05/10/2025 23:56:12 Cette version de la page est en cache (à la date du 05/10/2025 23:56:12) afin d'accélérer le traitement.Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la version plus récente de la page.
Document créé le 19/03/2002, dernière modification le 07/04/2023
Source du document imprimé : https://www.gaudry.be/matrices2.html
L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.


