Opérations sur les matrices
Egalité de matrices
Définition
Deux matrices A = (aij) et B = (bij) sont égales si
- elles sont de même format.
- aij = bij pour tout i et j.
Somme de deux matrices
Définition
Soit deux matrices A = (aij) et B = (bij), la somme des deux matrices est une matrice C = (cij)
- de même format.
- telle que cij = aij + bij pour tout i et j.
Exemple
Soit A et B les matrices suivantes :
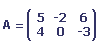
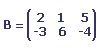
La somme des deux matrices est la matrice suivante :
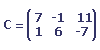
Remarque: l'addition est commutative (A+B=B+A).
Différence de deux matrices
Définition
Soit deux matrices A = (aij) et B = (bij), la différence des deux matrices est une matrice C = (cij)
- de même format.
- telle que cij = aij - bij pour tout i et j.
Exemple
Soit A et B les matrices suivantes :
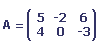
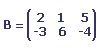
La différence des deux matrices est la matrice suivante :
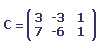
Remarques :
- La différence n'est pas commutative.
- A-B = -(B-A).
Produit d'une matrice par un scalaire
Définition
Soit une matrice quelconque A = (aij), et un scalaire ß, le produit des deux est une matrice B = (bij)
- de même format que A.
- telle que bij = ßaij pour tout i et j.
Exemple
Soit A la matrice suivantes:
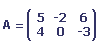
Le produit de la matrices et du scalaire 2 est la matrice suivante:
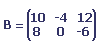
Produit de deux matrices
Définition
Soit deux matrices A = (aij) de format m*n, et B = (bij) de format n*p,
le produit des deux matrices est une matrice C = (cij)
- de format m*p.
- telle que cij est le produit de la ligne i de A par la colonne j de B pour tout i et j.
Exemple
Soit A et B les matrices suivantes:
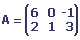
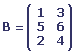
Le produit des deux matrices est la matrice suivante:
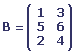
Remarque:
- Le produit matriciel n'est pas commutatif.
Version en cache
21/11/2024 09:38:58 Cette version de la page est en cache (à la date du 21/11/2024 09:38:58) afin d'accélérer le traitement. Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la dernère version de la page.Document créé le 19/03/2002, dernière modification le 26/10/2018
Source du document imprimé : https://www.gaudry.be/matrices-operations.html
L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.
