Demi additionneur binaire (half-adder)
Introduction
L'addition et la soustraction sont deux opérations arithmétiques de base. Nous allons donc tenter de comprendre comment l'ordinateur peut effectuer une addition.
En base 2, l'addition de deux bits correspond à ceci:
- 0 + 0 = 00
- 0 + 1 = 01
- 1 + 0 = 01
- 1 + 1 = 10
Décomposition du principe d'addition
Nous pouvons comparer cette addition avec une addition décimale, dans la mesure où il est possible d'avoir un report; rappelons nous l'addition des chiffres 5 et 6 en calcul écrit en base 10:
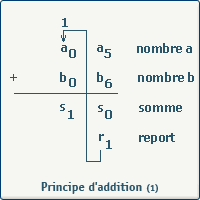
A partir du moment où un report intervient, nous devons envisager qu'il existe pour toute addition un report en entrée, et un report en sortie.
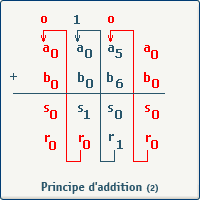
Le premier et le dernier report (en rouge dans le schéma) ont donc la valeur zéro. Il nous suffira donc d'initialiser le premier report à zéro; et le dernier report nous indiquera, dans le cas où il sera différent de zéro, qu'il y a dépassement de capacité (overflow).
Ceci nous permet de découper une addition complexe en une séquence utilisant à chaque fois le même traitement, ce que nous détaillerons dans la partie électronique.
L'addition des deux bits de bas poids (LSB: Least Significant Bit) a0 et b0, donne un résultat partiel s0 et une retenue r0. On forme ensuite la somme des deux bits a1 et b1 et de la retenue r0. Nous obtenons un résultat partiel s1 et une retenue r1. Et ainsi de suite, nous obtenons un résultat sur quatre bits S et une retenue r3.
Principe d'addition binaire: résumé
La figure suivante montre la décomposition de l'addition de deux nombres binaires de quatre bits.
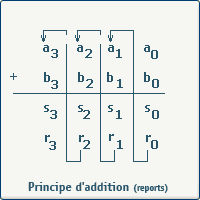
Schéma et table de vérité
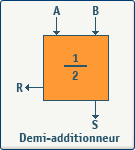
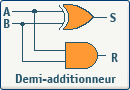
En entrée, nous avons les deux nombres à additionner (A et B), et en sortie, La somme (S) et le report (R). Ce module se nomme demi additionneur (half-adder), et nous pouvons constater qu'il ne tient pas compte du report d'entrée. Voyons donc la table de vérité :
Nous pouvons tirer certaines conclusions de cette table de vérité:
- S = A . B + A . B= A Å B
- R = A . B
Circuit logique du demi additionneur
Version en cache
04/10/2025 15:51:01 Cette version de la page est en cache (à la date du 04/10/2025 15:51:01) afin d'accélérer le traitement.Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la version plus récente de la page.
Document créé le 19/03/2002, dernière modification le 26/10/2018
Source du document imprimé : https://www.gaudry.be/logique-half-adder.html
L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.
Références
Ces références et liens indiquent des documents consultés lors de la rédaction de cette page, ou qui peuvent apporter un complément d'information, mais les auteurs de ces sources ne peuvent être tenus responsables du contenu de cette page.
L'auteur de ce site est seul responsable de la manière dont sont présentés ici les différents concepts, et des libertés qui sont prises avec les ouvrages de référence. N'oubliez pas que vous devez croiser les informations de sources multiples afin de diminuer les risques d'erreurs.




