Opérateurs logiques
- Opérateur de négation : NOT
- Opérateur de conjonction : AND
- Opérateurs de disjonction : OR et XOR
- Opérateurs d'implication
- Opérateurs d'équivalence
NOT : opérateur de négation
Notation de l'opérateur NOT
Soit p une proposition logique, la négation de p se notera ¬p, ou ~p, ou p, ou NOT(p)1.
Dans la mesure du possible, j'utiliserai la notation p; mais dans le cas par exemple d'une double négation, j'utiliserai la notation ¬¬p (simplement parce que je n'ai pas trouvé le moyen de surligner deux fois un caractère...).
Définition de l'opérateur NOT
p = vrai <=> p = faux
p = faux <=> p = vrai
Table de vérité de l'opérateur NOT
les valeurs sont purement et simplement inversées; nous pouvons parler de négation
Exemple de l'opérateur NOT
Soit la proposition (instruction) suivante:
if (a>b) printf("%d", a); else a++;
La négation ("!" en langage c) de la proposition donne:
if (!(a>b)) printf("%d",a); a++;
Remarques:
- En modifiant l'ordre des instructions, la négation est annulée:
if (!(a>b)) a++; else printf("%d", a); - Nous pouvons nier la proposition sans utiliser l'opérateur de négation:
if (a>b) a++; else printf("%d", a); est égal à if (!(a>b)) printf("%d",a); a++;
Propriétés de l'opérateur NOT
Une double négation s'annule: ¬¬p = p.
Exemple: "if (!(!(a>b))) printf("%d",a); a++;" est égal à "if (a>b)printf("%d",a); a++;"
L'opérateur logique NOT en électricité
L'équivalent en électricité de l'opérateur logique de négation est l'inverseur.
L'opérateur logique NOT en électronique
Notation américaine: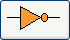
Notation européenne: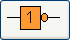
Remarque
L'opérateur de négation porte sur une seule proposition, même si cette dernière peut être composée d'opérations, ou être très complexe.
AND : opérateur de conjonction
Notation de l'opérateur AND
Soit p et q des propositions logiques, leur conjonction se notera p ^ q, ou p . q (attention: il ne s'agit pas ici d'algèbre traditionnel).
Définition de l'opérateur AND
p . q = vrai <=> p = vrai ET q = vrai
Table de vérité de l'opérateur AND
Nous pouvons donc en déduire que le zéro (valeur faux) est absorbant, comme en multiplication dans l'algèbre traditionnel.
Exemple de l'opérateur AND
if (a>10 && a<20) printf("%d", a);
Les deux conditions doivent être réunies pour que l'instruction soit exécutée; si une seule (ou aucune des deux) condition est réunie, l'instruction n'est pas exécutée.
En langage c ce type d'opérateur est figuré par la suite de caractères suivante: &&.
Dans notre exemple, les valeurs de 11 à 19 réunissent les conditions pour l'impression vers le fichier de sortie standard (l'écran).
Propriétés de l'opérateur AND
Soit 1 une tautologie et 0 une ineptie:
- p . p = p
- p . p = 0
- p . i = 0 (car p . 0 = 0)
- p . t = p (car p . 1 = p)
- p . q = q . p
- (p . q) . r = p . (q . r)
Démonstration de (p . q) . r = p . (q . r)
L'opérateur logique AND en électricité
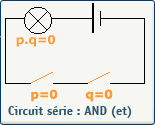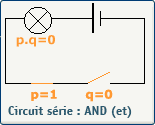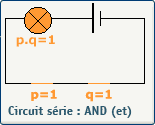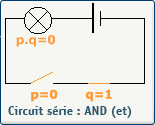
L'opérateur logique AND en électronique
Notation américaine: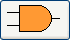
Notation européenne: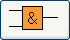
OR : opérateur de disjonction
Notation de l'opérateur OR
Soit p et q des propositions logiques, le OU inclusif se notera p + q, ou p v q.
Définition de l'opérateur OR
p + q = vrai si p ou q = vrai.
p + q = faux <=> p et q = faux.
Table de vérité de l'opérateur OR
Nous pouvons donc en déduire que le 1 (valeur vrai) est absorbant.
Exemple de l'opérateur OR
if ((a>5) || (b>10)) instruction1;
else instruction2;
a = 6 et b = 11 => instruction1
a = 6 et b = 6 => instruction1
a = 4 et b = 6 => instruction2
a = 4 et b = 11 => instruction1
Propriétés de l'opérateur OR
Soit 1 une tautologie et 0 une ineptie:
- p + p = p
- p + p = 1
- p + 1 = 1
- p + 0 = p
- p + q = q + p
- (p + q) + r = p + (q + r)
L'opérateur logique OR en électricité
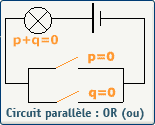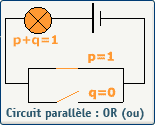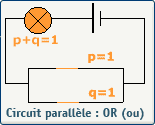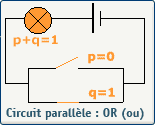
L'opérateur logique OR en électronique
Notation américaine:
Notation européenne: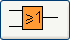
XOR : opérateur de disjonction
Notation de l'opérateur XOR
Soit p et q des propositions logiques, le OU exclusif se notera p ⊕ q, ou p v q.
Définition de l'opérateur XOR
Nous pouvons appeler XOR ou exclusif car il exclut le AND
p ⊕ q = p. q + p . q
p ⊕ q = ¬(pq + ¬p¬q)
p ⊕ q = (p + q) . ¬(pq)
p ⊕ q = (p + q)(¬p + ¬q)
Table de vérité de l'opérateur XOR
Propriétés de l'opérateur XOR
Soit 1 une tautologie et 0 une ineptie:
- p ⊕ p = 0
- p ⊕ p= 1
- p ⊕ 1 = p
- p ⊕ 0 = p
- p ⊕ q = q ⊕ p
- (p ⊕ q) ⊕ r = p ⊕ (q ⊕ r)
L'opérateur logique XOR en électronique
Notation américaine:
Notation européenne: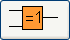
Opérateur d'implication
Notation de l'opérateur d'implication
Soit p et q des propositions logiques, l'équivalence se notera p => q.
Définition de l'opérateur d'implication
L'expression "p implique q" revient à nier l'antécédent et ajouter le conséquent. La proposition "p" est l'antécédent, et la proposition "q" est le conséquent. p => q ⇔ p + q
« Mais qu'est-ce qu'il dit? »
Nous pouvons dire que "p implique q" est faux seulement si "p" est vrai et que "q" est faux.
Table de vérité de l'opérateur d'implication
Opérateur d'équivalence
Notation de l'opérateur d'équivalence
Soit p et q des propositions logiques, l'équivalence se notera p ° q, ou p ⇔ q.
Table de vérité de l'opérateur d'équivalence
Exemple de l'opérateur d'équivalence
p = "ce triangle est équilatéral"
q = "ce triangle a trois côtés égaux"
p <=> q
Propriétés de l'opérateur d'équivalence
- (p <=> q) ⇔p. q+ p + q
- (p <=> q) ⇔p ⊕ q
- (p <=> q) ⇔(p => q) . (q => p)
Démonstration algébrique de (p <=> q) ⇔(p => q) . (q => p)
(p => q) . (q => p) ⇔(p+ q) . (q+ q)
⇔p. q+ p. p + q . q+ q . p
⇔p. q+ q . p ⇔(p <=> q) (cf. propriété1)
cqfd: (p => q) . (q => p) ⇔ (p <=> q)
Version en cache
04/10/2025 03:41:37 Cette version de la page est en cache (à la date du 04/10/2025 03:41:37) afin d'accélérer le traitement.Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la version plus récente de la page.
Document créé le 19/03/2002, dernière modification le 26/10/2018
Source du document imprimé : https://www.gaudry.be/logique-boole-operateurs.html
L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.
- ↑ Notation de la négation : Normalement la lettre p doit s'afficher avec un trait au dessus. Cependant, il est possible que des problèmes d'affichage ne permettent pas de voir le trait.


