Graphes : introduction

Sommaire du document

Avant de commencer

 pff, j’me souviens plus trop bien des opérations de booléens , un petit coup d’œil vers le chapitre « logique »…

 hého c’est quoi ces hiéroglyphes ?  un petit rappel pour se souvenir que la notation ensembliste ne se récite pas à la lueur des bougies au dessus d’un chaudron fumant.

 Bheu, c’est quoi une matrice ? , un petit détour vers les explications relatives aux matrices s’impose.

Quelques notations et termes

Un graphe est une représentation, une modélisation de nombreux problèmes.

Un graphe est avant tout un ensemble de points, que nous appellerons nœuds ou sommets (cela ne définit pas encore notre graphe, mais c’est un bon point de départ).

Nous pouvons relier certains de ces nœuds entre eux, et d’autres peuvent également se trouver isolés.

Ce qui nous intéresse est la relation qui existe entre les sommets, mais pas leurs positions exactes. Nous pouvons donc représenter de nombreuses manières différentes un même graphe. Deux graphes sont considérés comme isomorphes (identiques) s'ils comportent les mêmes ensembles de paires^[1] ou de couples^[2] sur le même ensemble X (ensemble des sommets).

Comme nous relions des nœuds, nous utiliserons des paires ou des couples pour désigner cette relation. Par exemple, le lien entre les sommets 1 et 2 s’écrira (1,2).

Selon que le sens dans lequel nous relions ces nœuds ou sommets soit important ou pas, nous nous trouverons en face de graphes orientés ou non orientés^[3]. Cette classification dichotomique^[4] des graphes nous poussera à nommer de manière différente certains éléments :

Dans le cas d’un arc^[2], nous devons spécifier par une flèche le sens de la relation entre les deux sommets. L’ordre dans lequel les sommets sont représentés au sein du couple est ici important, alors que pour un graphe non orienté la représentation est commutative^[13].

Quelques conventions qui seront utilisées au cours des pages suivantes :

• Notation G(X,A)
  • G = Graphe
  • X = Ensemble des sommets X={x₁, x₂, ... ,x_n}
  • A = Ensemble des arêtes si G est non-orienté (paires), ensemble des arcs si G est orienté (couples)
    A={a₁, a₂, ... , a_n}, ∀ a∈A ⇒ a={x, y}, x∈X ∧ y∈X
• G(X,A) = |{X}| = n : Cardinalité de l’ensemble des sommets. Parfois aussi représenté par #{X} = n.
  Nous devrions dire qu’il s’agit d’un graphe d’ordre n, mais par abus de langage nous disons souvent que le graphe est de taille n, ce qui n’est pas tout à fait correct, car la taille du graphe est m, défini ci-dessous.
• G(X,A) = |{A}| = m : Cardinalité de l’ensemble des arêtes ou des arcs. Il s'agit de la taille du graphe.

Relations entre n et m

Nous pouvons observer qu’il existe une étroite relation entre la cardinalité de l’ensemble des sommets(n) et la cardinalité de l’ensemble des arêtes^[1] ou des arcs^[2] (m)

Quand n devient très important, nous pouvons résumer le tableau en deux cas, car ajouter ou supprimer 1 à un très grand nombre est insignifiant :

• Graphe orienté m ≤ n²
• Graphe non-orienté m ≤ n²/2

Nous verrons aussi d'autres relations entre m et n lors des composantes simplement connexes.

Graphe simple et multigraphe

Dans le cas d'un graphe simple non-orienté, nous trouvons au maximum une arête, et maximum deux arcs (un pour chaque sens) pour un graphe simple orienté.

Dans le cas d'un multigraphe (ou p-graphe), nous pouvons avoir plus d'une arête, ou plus de deux arcs entre deux sommets.

Graphe valué

Un graphe valué est un graphe pour lequel nous associons une valeur à chaque arête^[16].

Nous pouvons aussi parfois utiliser le terme "graphes pondérés", ce qui signifie exactement la même chose (ce terme dérive de la pondération des arêtes).

La pondération d'une arête^[2] est une valeur associée à cette arête, qui correspond au coût (ou poids) que représente le passage par cette arête.

Précédent et suivant

Pour un arc (x,y)^[2], le sommet x est le précédent de y, et le sommet y est le suivant de x.

Par convention, nous tenterons de limiter l'usage des termes "précédents" et "suivants" aux sommets qui sont reliés par une chaîne de longueur 1^[17] avec le sommet courant. Pour l'ensemble des sommets qui précèdent ou suivent dans la hiérarchie, nous emploierons les termes de "prédécesseurs" et "successeurs".

Chaîne

Une chaîne est une suite finie de sommets reliés entre eux à chaque fois par une arête. Nous pouvons passer plusieurs fois par un même sommet dans une chaîne.

La longueur d'une chaîne est le nombre des arêtes qui la compose.

La valeur d'une chaîne pour un graphe valué est la somme des valeurs des arcs qui la compose.

Une chaîne simple est une chaîne pour laquelle nous n'utilisons qu'une seule fois chaque arête de la chaîne.

Une chaîne eulérienne est une chaîne simple pour laquelle nous utilisons toutes les arêtes du graphe.

Une chaîne hamiltonienne est une chaîne pour laquelle nous utilisons tous les sommets du graphe, en passant une et une seule fois par chaque sommet.

Nous pouvons aussi appliquer les qualificatifs eulérien et hamiltonnien aux cycles, et aux graphes en entier, qui remplissent ces conditions.

Distance

La distance entre deux sommets est la longueur de la plus petite chaîne qui relie ces deux sommets.

Arbre

Un arbre est un graphe connexe, sans cycle, simple, et sans boucle.
Vous pouvez aussi consulter la page d'exemples et d'exercices sur les arbres et les graphes.

Incidence

Une arête^[16] (a) est incidente à un sommet (s) si le sommet est une des extrémités de a. La réciprocité est vraie, car ∀a incident à s ⇒ s incident à a.

Nous pouvons avoir des arcs^[2] incidents à un sommet vers l'intérieur, ou des arcs incidents à un sommet vers l'extérieur.

• Soit a=(x,y)
  • a est incident à x vers l'extérieur (a part de x vers l'extérieur)
  • a est incident à y vers l'intérieur (a arrive dans y)

Adjacences

Pour une paire ou un couple (x,y), les sommets x et y sont adjacents.

Des arêtes^[16] a(x,y) et b(y,z) sont aussi dits adjacents car ils possèdent en commun le sommet y.

Matrice associée à un graphe

La matrice est un des moyens de représenter un graphe, très pratique en mathématique, mais assez coûteux en informatique (nécessite beaucoup de place en mémoire).

Nous utiliserons une matrice booléenne (remplie uniquement de 0 et de 1) M de dimension n*n telle que M[i,j] =1 si et seulement si (i,j) ∈ A.

Graphe complet

Un graphe complet est un graphe dont la matrice associée vérifie M[i,j]+M[i,j]≥1 si i≠j.

Pour être plus clair, un graphe est complet si chaque sommet est relié à chacun des autres sommets par une arête.

Un graphe complet est donc toujours simplement connexe.

Nous pouvons trouver un chemin hamiltonien dans tout graphe complet^[18].

Application multivoque

L'application multivoque du graphe G(X,A) (notée par le signe gamma : Γ) est la relation dans X entre un sommet x et l'ensemble de ses suivants (en orienté) ou de ses adjacents (en non-orienté).
Γ(x) = {y|((x,y)∈ A}

Application réciproque

L'application réciproque du graphe G(X,A) (notée Γ^-1) est la relation dans X entre un sommet x et l'ensemble de ses précédents (en orienté) ou de ses adjacents (en non-orienté).
Γ^-1(x) = {y|((y,x)∈ A}

Nous pouvons constater que Γ=Γ^-1 dans le cas d'un graphe non-orienté.

Degré

Soit G = (X,A) un graphe simple, et x un sommet de G. Le degré de x, noté d(x) (ou d_G(x) pour signaler que c'est le degré de x qui appartient au graphe G), est le nombre d'arêtes^[16] incidentes à x.

Lorsque d(x)=0, nous pouvons dire que x est un « sommet isolé » (en anglais, “isolated vertex”), et si d(x)=1 nous pouvons dire que x est un « sommet pendant » (en anglais, “leaf vertex”).

Attention : un arc a(x,x) (une boucle) est noté deux fois, mais compté une seule fois dans le degré.

Dans le cas d'un graphe orienté, nous pouvons classer les degrés d'un sommet en deux catégories :

• « Degré intérieur »^[21] : les arcs qui ont pour destination ce sommet (extrémité initiale). Noté d(x)_int ou d^-(x)^[22]
  Nous retrouvons parfois le terme degré entrant.
• « Degré extérieur »^[23] : les arcs qui ont pour origine ce sommet (extrémité finale). Noté d(x)_ext ou d⁺(x)
  Nous retrouvons parfois le terme degré sortant.

• Un sommet de degré intérieur 0 et de degré extérieur > à 0 est un « sommet source » (en anglais, “source vertex”).
• Un sommet de degré extérieur 0 et de degré intérieur > à 0 est un « sommet puit » (en anglais, “sink vertex”).

Calcul du degré des sommets dans un graphe

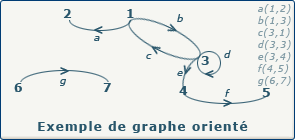
Dans l'exemple ci-dessus, nous avons un graphe simple orienté, avec 7 sommets, et 7 arcs. Comme nous avons une représentation graphique, nous pouvons aisément calculer les degrés des différents sommets.

d(1) : (1, 2) + (1, 3) + (3, 1) = a+b+c = 3 où a et b sont des degrés extérieurs(d_ext) et c est un degré intérieur(d_int).

Nous pouvons facilement déduire la formule d(x) = d(x)_ext + d(x)_ext
Cette formule s'applique bien au sommet 2 (d(2) = 0+1 = 1), mais qu'en est-il pour le sommet 3?

d(3)_ext = c + d + e = 3
d(3)_int = b + d = 2

⇒d(3) = 3 + 2 = 5, mais nous ne trouvons que 4 arcs pour le sommet 3.
Comme nous avons une boucle (l'arc d) pour le sommet 3, nous comptons à la fois la boucle en tant que degré intérieur car d a bien pour destination le sommet 3 et en tant que degré extérieur car d a bien pour origine le sommet 3.

Afin d'éviter de compter deux fois une boucle, nous devons modifier notre formule en utilisant une fonction indicatrice I qui nous retourne 1 si nous sommes en présence d'une boucle (origine et destination identique), sinon zéro.

d(x) = d(x)_ext + d(x)_ext - I(x)

Ce qui nous donne :

• d(1) = 2 + 1 - 0 = 3
• d(2) = 0 + 1 - 0 = 1
• d(3) = 3 + 2 - 1 = 4
• d(4) = 1 + 1 - 0 = 2
• d(5) = 0 + 1 - 0 = 1
• d(6) = 1 + 0 - 0 = 1
• d(7) = 0 + 1 - 0 = 1

Lemme des poignées de mains

Soit G = (X,A) un graphe simple, nous avons 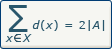Ce qui signifie que la somme des degrés des sommets d'un graphe est égale à deux fois le nombre d'arêtes,car chaque arête a(x, y) est comptée deux fois, une fois lors du calcul du degré de x et une fois lors du calcul du degré de y.

Nous pouvons aussi représenter cette formule de la manière suivante : 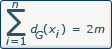car |A| et m correspondent à la cardinalité de l'ensemble des arêtes, n correspond à la cardinalité de X (l'ensemble des sommets).

Lors des calculs de degrés nous comptions chaque boucle une seule fois dans le degré, mais ici une boucle doit être comptée deux fois (ce qui correspond à la formule initiale) pour le lemme des poignées de mains. Dès lors, le lemme des poignées de mains reste valable pour les multigraphes avec boucles.

Démonstration du lemme des poignées de mains

Graphe régulier

Nous pouvons dire d'un graphe simple qu'il est régulier de degré r si tous les sommets du graphe sont de degré r.

Densité d'un graphe

La densité du graphe est la proportion entre le nombre d’arêtes ou d’arcs (m) et le nombre total de liens possibles (mmax).

Composantes simplement connexes

Nous pouvons définir la connexité simple de la manière suivante : ∀x, ∀y : ∃ chaîne entre x et y.

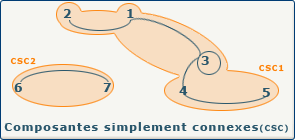
La notion « simplement connexe » (en anglais, “weakly connected”) peut s'appliquer à l'ensemble du graphe (si pour tout couple de sommet x et y il existe une chaîne entre x et y), ou à une partie du graphe (nous parlons alors de composante simplement connexe). Cette notion de connexité simple est assez évidente lorsque nous avons peu de sommets et que nous représentons graphiquement le graphe, comme dans l'exemple ci dessous. Nous pouvons dès lors constater qu'au sein d'une composante simplement connexe (csc) chaque sommet est accessible au départ de n'importe quel sommet de la composante.

Si m ≥ n-1, toutes les arêtes^[16]sont reliées. Dans ce cas, nous avons une seule composante simplement connexe.

Si m < n-1, nous nous trouvons en présence de plus d'une composante simplement connexe.

L'exemple ci-contre montre que notre graphe comporte deux composantes simplement connexes.
Les sommets {1, 2, 3, 4, 5} forment une composante simplement connexe, et les sommets {6,7} forment la deuxième.

Cet exemple montre un graphe simple non-orienté. Qu'en est-il pour les graphes orientés ?

Dans notre premier exemple, si nous appliquons cete définition le ne comportait qu'une seule csc composée des sommets {1,3}, et cinq csc composées chacune d'un seul sommet ({2}, {4}, {5}, {6}, et {7}). Or ce n'est pas le cas.
Dans le cas de graphes orientés nous devons considérer les arcs comme des arêtes, et nous pouvons ensuite appliquer la définition de la csc qui dit que chaque sommet de la composante simplement connexe doit être accessible depuis n'importe quel sommet de la même composante.

Si notre graphe comportait un huitième sommet qui n'était relié à aucun autre sommet, ou s'il était relié à lui même par une boucle, il serait considéré comme une composante simplement connexe, car tout sommet isolé respecte la définition de la csc. Nous aurions alors trois composantes simplement connexes.

Un graphe complet est donc toujours simplement connexe, mais tout graphe simplement connexe n'est pas forcément complet, car la connexité relie x et y par des chaînes (peu importe la longueur), mais un graphe complet a la contrainte que x et y soient reliés par seulement des chaînes (ou chemins) de longueur 1.

Composantes fortement connexes

Nous pouvons définir la connexité forte de la manière suivante : ∀x, ∀y : ∃ chemin entre x et y et ∃ chemin entre y et x.

Nous pourrions considérer chaque composante simplement connexe d'un graphe non-orienté comme une composante « fortement connexe » (en anglais, “strongly connected”) de ce graphe, en considérant chaque arête comme deux arcs de sens opposés, mais nous réserverons uniquement la connexité forte aux graphes orientés.

Comme dans le cas de la connexité simple, la connexité forte peut s'appliquer à un graphe en entier (graphe fortement connexe), ou le graphe peut être décomposé en composantes fortement connexes.

Un graphe complet est donc toujours un graphe fortement connexe (car nous pouvons remplacer les arêtes par deux arcs aux directions opposées), mais l'inverse n'est pas toujours vrai (pour être complet, les chemins doivent avoir une longueur 1).

De par sa définition, un graphe fortement connexe contient forcément des circuits.

Pour chercher les composantes fortement connexes d'un graphe, nous pouvons utiliser les algorithmes de Foulkes ou de Malgrange.

Graphes et composantes connexes

Le fait de décomposer un graphe en composantes nous permet d'en simplifier la représentation et le traitement^[28].

Indice chromatique d'un graphe

L'indice chromatique d'un graphe est le nombre minimal de couleurs que nous devrons utiliser pour colorer les arêtes du graphe de telle sorte que deux arêtes adjacentes n'aient pas la même couleur.

Nombre chromatique d'un graphe

Le nombre chromatique d'un graphe est le nombre minimal de couleurs que nous devrons utiliser pour colorer les sommets du graphe de telle sorte que deux sommets adjacents n'aient pas la même couleur.

Notes

1. ↑^a,b Non-orientés : Ceci est valable seulement pour les graphes non-orientés
   
   
2. ↑^a,b,c,d,e,f Orientés : Ceci est valable seulement pour les graphes orientés
   
   
3. ↑ Graphe non-orienté : un graphe non-orienté peut être considéré selon certaines définitions comme un arc orienté symétrique (dans les deux sens)
   
   
4. ↑ Dichotomique : en deux parties
   
   
5. ↑^a,b sommet : correspond à “vertex, vertices » en anglais
   
   
6. ↑ paire : correspond à “pair » en anglais
   
   
7. ↑ arête : correspond à “edge » en anglais
   
   
8. ↑ arc : correspond à “arc » en anglais
   
   
9. ↑ chemin : correspond à “path » en anglais
   
   
10. ↑ parcours : correspond à “walk » en anglais
    
    
11. ↑ parcours : Bondy et Murty utilisent le terme parcours (walk) pour désigner un chemin dans lequel nous passons plusieurs fois par un même sommet ou un même arc. Nous retrouvons parfois aussi le terme promenade
    
    
12. ↑ cycle : correspond à “cycle » en anglais
    
    
13. ↑ Commutativité : l’ordre au sein de la paire n’est pas important, et l’arête (1,2) peut s’écrire (2,1). Je ne dénoncerais personne, mais le moyen mnémotechnique qui nous a été suggéré est que dans un couple un des deux a plus à dire que l’autre au sein de la relation.
    
    
14. ↑ m ≤ n2 : car pour un graphe orienté avec boucles chaque sommet peut être relié à chacun des autres sommets, et à lui-même, donc n * n
    
    
15. ↑ m ≤ n*(n-1) : car nous avons n*n (n2) avec les boucles, et nous retirons 1 pour la boucle
    
    
16. ↑^a,b,c,d,e Arête ou arc : Nous utilisons ici le terme arête pour désigner aussi bien une arête qu'un arc
    
    
17. ↑ Chaîne de longueur 1 : Ici pour désigner les sommets qui suivent ou précèdent directement le sommet courant (les enfants ou parents directs).
    
    
18. ↑ Théorème de König-Rédei : Tout graphe complet admet un chemin hamiltonien. Dénes König (1884-1944) et László Rédei (1900-1980) sont des mathématiciens hongrois.
    
    
19. ↑ sommet isolé : correspond à “isolated vertex » en anglais
    
    
20. ↑ sommet pendant : correspond à “leaf vertex » en anglais
    
    
21. ↑ Degré intérieur : correspond à “iner degree, in degree » en anglais
    
    
22. ↑ d_G^-(x) : Je n'utiliserais pas ce type de notation, car j'ai rencontré au cours de mes recherches d'informations autant de fois le signe - pour désigner un degré intérieur que pour désigner un degré extérieur. Cette source d'erreur est évitée en utilisant "int" et "ext".
    
    
23. ↑ Degré extérieur : correspond à “outer degree, out degree » en anglais
    
    
24. ↑ sommet source : correspond à “source vertex » en anglais
    
    
25. ↑ sommet puit : correspond à “sink vertex » en anglais
    
    
26. ↑ simplement connexe : correspond à “weakly connected » en anglais
    
    
27. ↑ fortement connexe : correspond à “strongly connected » en anglais
    
    
28. ↑ Décomposer pour simplifier : Voir aussi le principe de diviser pour régner
    
    

Références

1. INFOB321 - Théorie des graphes : JP Leclercq, Cours de Théorie des Graphes et réseaux de Petri (Septembre 2008)
2. Shortest paths in graphs : Zoltan KASA (07/11/09)
3. Théorie des graphes : Wikiversity, Théorie des graphes : Fondements (version 07/11/09)
4. Graphe et Complexité : Université Pierre Mendes Françe - Grenoble, Graphe et Complexité : cours
5. Graph Theory with Applications : J.A. Bondy and U.S.R. Murty

Ces références et liens indiquent des documents consultés lors de la rédaction de cette page, ou qui peuvent apporter un complément d'information, mais les auteurs de ces sources ne peuvent être tenus responsables du contenu de cette page.
L'auteur de ce site est seul responsable de la manière dont sont présentés ici les différents concepts, et des libertés qui sont prises avec les ouvrages de référence. N'oubliez pas que vous devez croiser les informations de sources multiples afin de diminuer les risques d'erreurs.

Structure du document