Composantes Fortement Connexes

Composantes simplement connexes

Nous pouvons définir la connexité simple de la manière suivante : ∀x, ∀y : ∃ chaîne entre x et y.

La notion « simplement connexe » (en anglais, “weakly connected”) peut s'appliquer à l'ensemble du graphe (si pour tout couple de sommet x et y il existe une chaîne entre x et y), ou à une partie du graphe (nous parlons alors de composante simplement connexe). Cette notion de connexité simple est assez évidente lorsque nous avons peu de sommets et que nous représentons graphiquement le graphe, comme dans l'exemple ci dessous. Nous pouvons dès lors constater qu'au sein d'une composante simplement connexe (csc) chaque sommet est accessible au départ de n'importe quel sommet de la composante.

Si m ≥ n-1, toutes les arêtes²sont reliées. Dans ce cas, nous avons une seule composante simplement connexe.

Si m < n-1, nous nous trouvons en présence de plus d'une composante simplement connexe.

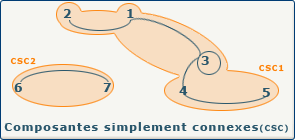
L'exemple ci-contre montre que notre graphe comporte deux composantes simplement connexes.
Les sommets {1, 2, 3, 4, 5} forment une composante simplement connexe, et les sommets {6,7} forment la deuxième.

Cet exemple montre un graphe simple non-orienté. Qu'en est-il pour les graphes orientés ?

Dans notre premier exemple, si nous appliquons cete définition le ne comportait qu'une seule csc composée des sommets {1,3}, et cinq csc composées chacune d'un seul sommet ({2}, {4}, {5}, {6}, et {7}). Or ce n'est pas le cas.
Dans le cas de graphes orientés nous devons considérer les arcs comme des arêtes, et nous pouvons ensuite appliquer la définition de la csc qui dit que chaque sommet de la composante simplement connexe doit être accessible depuis n'importe quel sommet de la même composante.

Si notre graphe comportait un huitième sommet qui n'était relié à aucun autre sommet, ou s'il était relié à lui même par une boucle, il serait considéré comme une composante simplement connexe, car tout sommet isolé respecte la définition de la csc. Nous aurions alors trois composantes simplement connexes.

Un graphe complet est donc toujours simplement connexe, mais tout graphe simplement connexe n'est pas forcément complet, car la connexité relie x et y par des chaînes (peu importe la longueur), mais un graphe complet a la contrainte que x et y soient reliés par seulement des chaînes (ou chemins) de longueur 1.

Table des matières Haut

Composantes fortement connexes

Nous pouvons définir la connexité forte de la manière suivante : ∀x, ∀y : ∃ chemin entre x et y et ∃ chemin entre y et x.

Nous pourrions considérer chaque composante simplement connexe d'un graphe non-orienté comme une composante « fortement connexe » (en anglais, “strongly connected”) de ce graphe, en considérant chaque arête comme deux arcs de sens opposés, mais nous réserverons uniquement la connexité forte aux graphes orientés.

Comme dans le cas de la connexité simple, la connexité forte peut s'appliquer à un graphe en entier (graphe fortement connexe), ou le graphe peut être décomposé en composantes fortement connexes.

Un graphe complet est donc toujours un graphe fortement connexe (car nous pouvons remplacer les arêtes par deux arcs aux directions opposées), mais l'inverse n'est pas toujours vrai (pour être complet, les chemins doivent avoir une longueur 1).

De par sa définition, un graphe fortement connexe contient forcément des circuits.

Pour chercher les composantes fortement connexes d'un graphe, nous pouvons utiliser les algorithmes de Foulkes ou de Malgrange.

Table des matières Haut

Fonctionnalités de l'algorithme de Foulkes

• L'algorithme de Foulkes permet de construire les composantes fortement connexes d'un graphe.

Caractéristiques de l'algorithme de Foulkes

L'algorithme de Foulkes présume que nous avons préalablement effectué une recherche de la fermeture transitive de notre graphe (par exemple avec l'algorithme de Warshall).

Si deux sommets appartiennent à la même composante fortement connexe, nous pouvons en déduire certaines similitudes au niveau de la matrice d'accessibilité (ils peuvent accéder au même ensemble de sommets). Nous devrons donc chercher au sein de la matrice de fermeture transitive les sommets pour lesquels la ligne dans cette matrice est identique. Ils appartiennent donc à la même composante fortement connexe.

Table des matières Haut

Complexité de l'algorithme de Foulkes

La complexité générale est de (n³) car le calcul de la matrice de fermeture transitive est déjà de (n³).

Fonctionnalités de l'algorithme de Malgrange

• L'algorithme de Malgrange permet de construire les composantes fortement connexes d'un graphe.

Caractéristiques de l'algorithme de Malgrange

• Choisir arbitrairement un sommet x
• Chercher les successeurs de x, soit S(x) au moyen de DFS
• Chercher les prédécesseurs de x, soit P(x) au moyen de DFS
• S(x) ∩P(x) nous donne la composante fortement connexe contenant x.

You are on the French version of the site, but your system indicates that you prefer to use the English language.
The entire site is not translated yet, but the menus and buttons on the interface are largely translated.

Would you like to reach the page in English?
Click here to continue in English: Consult the English version of this page

U bevindt zich op de Franse versie van de site, maar uw systeem geeft aan dat u liever de Nederlandse taal gebruikt.
De hele site is nog niet vertaald, maar de menu's en knoppen op de interface zijn grotendeels vertaald.

Wilt u de pagina in het Nederlands bereiken?
Klik hier om door te gaan in het Nederlands: Raadpleeg de Nederlandse versie van deze pagina

Sie befinden sich in der französischen Version der Website, Ihr System gibt jedoch an, dass Sie die deutsche Sprache bevorzugen.
Die gesamte Site ist noch nicht übersetzt, aber die Menüs und Schaltflächen auf der Benutzeroberfläche sind weitgehend übersetzt.

Möchten Sie die Seite auf Deutsch erreichen?
Klicken Sie hier, um fortzufahren: Konsultieren Sie die deutsche Version dieser Seite