No cache version.

Caching disabled. Default setting for this page:enabled (code LNG204)
If the display is too slow, you can disable the user mode to view the cached version.

Matrices particulières

Contents

Matrice carrée

Une matrice est appelée carrée lorsque les nombres de lignes et de colonnes sont identiques.

Exemple:

Matrice carrée

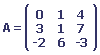
La matrice A possède trois lignes et trois colonnes, elle est donc carrée.

Contents Haut

Vecteur ligne

Un vecteur ligne est une matrice qui possède une seule ligne.

Exemple:

vecteur ligne

Contents Haut

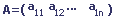
Vecteur colonne

Un vecteur colonne est une matrice qui possède une seule colonne.

Exemple:

vecteur colonne

Contents Haut

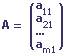
Matrice scalaire

Une matrice scalaire est une matrice qui ne possède qu'une seule ligne et une seule colonne (elle ne possède donc qu'un seul élément).

Exemple:

Matrice scalaire

Contents Haut

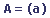
Matrice diagonale

Une matrice diagonale est une matrice carrée dont tous les éléments non compris dans la diagonale principale sont nuls.

Exemples:

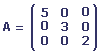Matrice diagonale ou 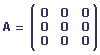Matrice diagonale (au minimum diagonale)

Contents Haut

Matrice identité

Une matrice identité (ou unité) est une matrice diagonale dont les éléments de la diagonale principale sont de valeur 1.

Matrice identité

Contents Haut

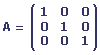
Matrice triangulaire

Une matrice triangulaire est une matrice carrée dont les éléments d'un même côté de la diagonale principale sont de valeur 0.

Matrice triangulaire supérieure

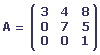
Matrice triangulaire supérieure

Matrice triangulaire inférieure

Matrice triangulaire inférieure

Contents Haut

Transposée d'une matrice

Nous obtenons la transposée d'une matrice en permutant les lignes et les colonnes:

Remarques:

  • La transposée de la matrice A se note donc tA.
  • La transposée de la matrice de format m*n est une matrice de format n*m.
  • Si tA=A, nous pouvons dire que la matrice est symétrique (elle doit donc être carrée).
  • Si tA=-A, nous pouvons dire que la matrice est antisymétrique.

English translation

You have asked to visit this site in English. For now, only the interface is translated, but not all the content yet.

If you want to help me in translations, your contribution is welcome. All you need to do is register on the site, and send me a message asking me to add you to the group of translators, which will give you the opportunity to translate the pages you want. A link at the bottom of each translated page indicates that you are the translator, and has a link to your profile.

Thank you in advance.

Document created the 19/03/2002, last modified the 07/04/2023
Source of the printed document:https://www.gaudry.be/en/matrices2.html

The infobrol is a personal site whose content is my sole responsibility. The text is available under CreativeCommons license (BY-NC-SA). More info on the terms of use and the author.