Opérations sur les matrices

Contents

Egalité de matrices

Définition

Deux matrices A = (aij) et B = (bij) sont égales si

  • elles sont de même format.
  • aij = bij pour tout i et j.

Somme de deux matrices

Définition

Soit deux matrices A = (aij) et B = (bij), la somme des deux matrices est une matrice C = (cij)

  • de même format.
  • telle que cij = aij + bij pour tout i et j.

Exemple

Soit A et B les matrices suivantes :

Matrice A
Matrice B

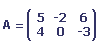
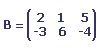
La somme des deux matrices est la matrice suivante :

Matrice C (somme des matrices A et B)

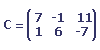
Remarque: l'addition est commutative (A+B=B+A).

Différence de deux matrices

Définition

Soit deux matrices A = (aij) et B = (bij), la différence des deux matrices est une matrice C = (cij)

  • de même format.
  • telle que cij = aij - bij pour tout i et j.

Exemple

Soit A et B les matrices suivantes :

Matrice A
Matrice B

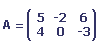
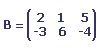
La différence des deux matrices est la matrice suivante :

Matrice C (différence des matrices A et B)

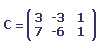
Remarques :

  • La différence n'est pas commutative.
  • A-B = -(B-A).

Produit d'une matrice par un scalaire

Définition

Soit une matrice quelconque A = (aij), et un scalaire ß, le produit des deux est une matrice B = (bij)

  • de même format que A.
  • telle que bij = ßaij pour tout i et j.

Exemple

Soit A la matrice suivantes:

Matrice A

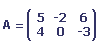
Le produit de la matrices et du scalaire 2 est la matrice suivante:

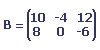
Matrice C (produit de la matrice A et du scalaire 2)

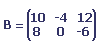
Produit de deux matrices

Définition

Soit deux matrices A = (aij) de format m*n, et B = (bij) de format n*p,
le produit des deux matrices est une matrice C = (cij)

  • de format m*p.
  • telle que cij est le produit de la ligne i de A par la colonne j de B pour tout i et j.

Exemple

Soit A et B les matrices suivantes:

Matrice A
Matrice B

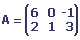
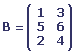
Le produit des deux matrices est la matrice suivante:

Matrice C (produit de deux matrices)

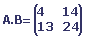
Remarque:

  • Le produit matriciel n'est pas commutatif.

English translation

You have asked to visit this site in English. For now, only the interface is translated, but not all the content yet.

If you want to help me in translations, your contribution is welcome. All you need to do is register on the site, and send me a message asking me to add you to the group of translators, which will give you the opportunity to translate the pages you want. A link at the bottom of each translated page indicates that you are the translator, and has a link to your profile.

Thank you in advance.

Document created the 19/03/2002, last modified the 26/10/2018
Source of the printed document:https://www.gaudry.be/en/matrices-operations.html

The infobrol is a personal site whose content is my sole responsibility. The text is available under CreativeCommons license (BY-NC-SA). More info on the terms of use and the author.