Exercices sur les matrices
1. Soit les matrices A et B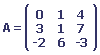
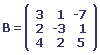
Nous devons calculer B - A ; 2A + B ; A . B ; B . A ; tA . tB.
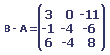
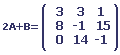
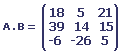
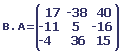
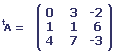
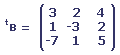
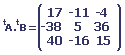
2. Un garagiste représente son inventaire de nouvelles voitures par une matrice de format 3 * 4.
Les nombres figurant dans les lignes concernent les voitures de marque X, Y et Z, tandis que les nombres des quatre colonnes ont trait respectivement aux deux portes, quatre portes, cinq portes et aux camionnettes.
Considérons les matrices suivantes:
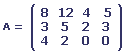
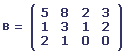
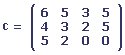
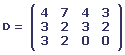
Si A représente l'inventaire au premier janvier de l'année dernière, B les ventes pendant le premier trimestre, C les voitures reçues pendant le deuxième trimestre et D les ventes pendant le deuxième trimestre, comment se présentait l'inventaire du garagiste au début du troisième trimestre (sous forme d'une matrice 3 * 4)?
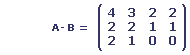
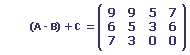
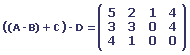
3. Une entreprise de construction a accepté la commande de six maisons, huit chalets et dix villas.
Les matériaux utilisés sont l'acier, le bois, le verre et la peinture.
Les quantités (en unités) à utiliser par ce genre d'habitation sont donnés dans le tableau suivant:
Nous devons représenter sous forme de matrices
La commande (format 1*3)

Les quantités de matériaux (format 3*4)
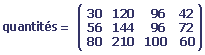
Les quantités totales de chaque matériau nécessaire pour le chantier (format 1*4)
Par multiplication:
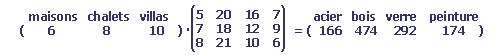
English translation
You have asked to visit this site in English. For now, only the interface is translated, but not all the content yet.If you want to help me in translations, your contribution is welcome. All you need to do is register on the site, and send me a message asking me to add you to the group of translators, which will give you the opportunity to translate the pages you want. A link at the bottom of each translated page indicates that you are the translator, and has a link to your profile.
Thank you in advance.
Document created the 19/03/2002, last modified the 26/10/2018
Source of the printed document:https://www.gaudry.be/en/matrices-exercices.html
The infobrol is a personal site whose content is my sole responsibility. The text is available under CreativeCommons license (BY-NC-SA). More info on the terms of use and the author.


