Graphes : matrice d'adjacence

Introduction

Nous utiliserons dans les exemples la notation définie lors de l'introduction aux graphes.

Principe de la matrice d'adjacence

$Graphes: matrice d'adjacence$

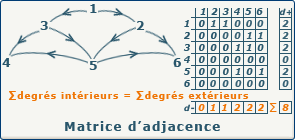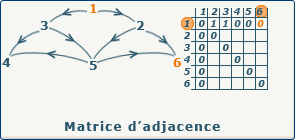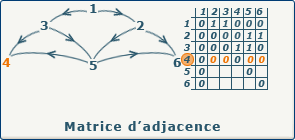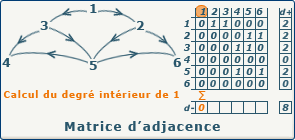
Nous pouvons représenter notre graphe G(X,A) sous la forme d'une matrice carrée de taille n*n. La ligne correspond au sommet de départ, et la colonne au sommet d'arrivée.

Ensuite, nous pouvons placer dans chaque case de notre matrice la valeur 0 ou 1 selon que le couple formé par l'indice de ligne et l'indice de colonne corresponde ou pas à un ensemble de A (en clair, 1 si l'arc existe dans le graphe). Ceci peut se traduire par la formule suivante : A_ij = 0 si (x_i,x_j)∉A, 1 si (x_i,x_j)∈A

Dans le cas d'un graphe non-orienté, notre matrice d'adjacence sera donc symétrique (x_ij=x_ji).

Nous pouvons trouver au maximum n! matrices d'adjacence pour notre graphe, selon l'ordre dans lequel nous considérons les sommets.

Algorithme de la matrice d'adjacence

Soient les matrices M, A, et B implémentées sous formes de tableaux de tableaux :

pour i variant_de 1 jusque n faire
	pour j variant_de 1 jusque n faire
		M[i,j] := 0;
		pour k variant_de 1 jusque n faire
			M[i,j] := M[i,j] &oplus; A[i,k] &otimes; B[k,j];
		fin pour
	fin pour
fin pour

Ce genre d'algorithme effectue le plus souvent le plus souvent le calcul suivant 0*0. Les deux boucles extérieures sont indispensables, mais nous pouvons par contre remplacer la boucle intérieure par les pointeurs d'arcs si ces derniers sont disponibles.

Contents Haut

Matrice de poids des arcs

$Matrice de poids des arcs$

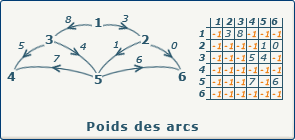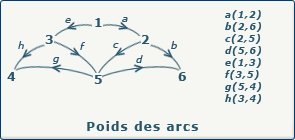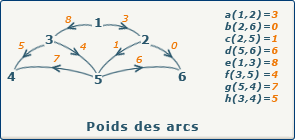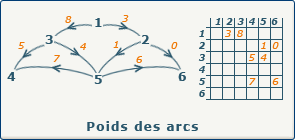
Si nous travaillons avec un graphe valué, au lieu de placer la valeur 1 quand un arc est présent, nous allons placer le poids (la valeur) de cet arc dans la case appropriée de la matrice.

Attention que dans ce cas, nous ne pouvons plus placer la valeur 0 pour signaler un arc inexistant, car cela représenterait un arc existant, de poids 0. Nous allons donc choisir arbitrairement une valeur non utilisée (par exemple -1 si nous avons la certitude que toutes nos valeurs sont positives).

English translation

You have asked to visit this site in English. For now, only the interface is translated, but not all the content yet.

If you want to help me in translations, your contribution is welcome. All you need to do is register on the site, and send me a message asking me to add you to the group of translators, which will give you the opportunity to translate the pages you want. A link at the bottom of each translated page indicates that you are the translator, and has a link to your profile.

Thank you in advance.

Document created the 11/11/2009, last modified the 26/10/2018
Source of the printed document:https://www.gaudry.be/en/graphes-matrice-adjacence.html

The infobrol is a personal site whose content is my sole responsibility. The text is available under CreativeCommons license (BY-NC-SA). More info on the terms of use and the author.

References

INFOB321 - Théorie des graphes : JP Leclercq, Cours de Théorie des Graphes et réseaux de Petri (September 2008)

These references and links indicate documents consulted during the writing of this page, or which may provide additional information, but the authors of these sources can not be held responsible for the content of this page.
The author This site is solely responsible for the way in which the various concepts, and the freedoms that are taken with the reference works, are presented here. Remember that you must cross multiple source information to reduce the risk of errors.

Contents Haut