Demi additionneur binaire (half-adder)
Introduction
L'addition et la soustraction sont deux opérations arithmétiques de base. Nous allons donc tenter de comprendre comment l'ordinateur peut effectuer une addition.
En base 2, l'addition de deux bits correspond à ceci:
- 0 + 0 = 00
- 0 + 1 = 01
- 1 + 0 = 01
- 1 + 1 = 10
Décomposition du principe d'addition
Nous pouvons comparer cette addition avec une addition décimale, dans la mesure où il est possible d'avoir un report; rappelons nous l'addition des chiffres 5 et 6 en calcul écrit en base 10:
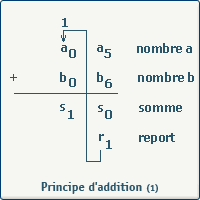
A partir du moment où un report intervient, nous devons envisager qu'il existe pour toute addition un report en entrée, et un report en sortie.
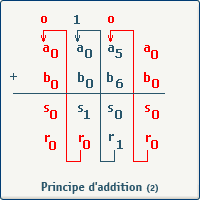
Le premier et le dernier report (en rouge dans le schéma) ont donc la valeur zéro. Il nous suffira donc d'initialiser le premier report à zéro; et le dernier report nous indiquera, dans le cas où il sera différent de zéro, qu'il y a dépassement de capacité (overflow).
Ceci nous permet de découper une addition complexe en une séquence utilisant à chaque fois le même traitement, ce que nous détaillerons dans la partie électronique.
L'addition des deux bits de bas poids (LSB: Least Significant Bit) a0 et b0, donne un résultat partiel s0 et une retenue r0. On forme ensuite la somme des deux bits a1 et b1 et de la retenue r0. Nous obtenons un résultat partiel s1 et une retenue r1. Et ainsi de suite, nous obtenons un résultat sur quatre bits S et une retenue r3.
Principe d'addition binaire: résumé
La figure suivante montre la décomposition de l'addition de deux nombres binaires de quatre bits.
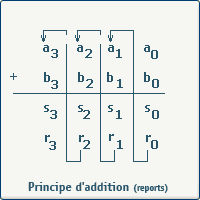
Schéma et table de vérité
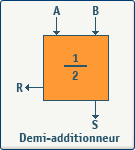
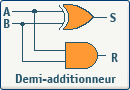
En entrée, nous avons les deux nombres à additionner (A et B), et en sortie, La somme (S) et le report (R). Ce module se nomme demi additionneur (half-adder), et nous pouvons constater qu'il ne tient pas compte du report d'entrée. Voyons donc la table de vérité :
Nous pouvons tirer certaines conclusions de cette table de vérité:
- S = A . B + A . B= A Å B
- R = A . B
Circuit logique du demi additionneur
Deutsche Übersetzung
Sie haben gebeten, diese Seite auf Deutsch zu besuchen. Momentan ist nur die Oberfläche übersetzt, aber noch nicht der gesamte Inhalt.Wenn Sie mir bei Übersetzungen helfen wollen, ist Ihr Beitrag willkommen. Alles, was Sie tun müssen, ist, sich auf der Website zu registrieren und mir eine Nachricht zu schicken, in der Sie gebeten werden, Sie der Gruppe der Übersetzer hinzuzufügen, die Ihnen die Möglichkeit gibt, die gewünschten Seiten zu übersetzen. Ein Link am Ende jeder übersetzten Seite zeigt an, dass Sie der Übersetzer sind und einen Link zu Ihrem Profil haben.
Vielen Dank im Voraus.
Dokument erstellt 19/03/2002, zuletzt geändert 26/10/2018
Quelle des gedruckten Dokuments:https://www.gaudry.be/de/logique-half-adder.html
Die Infobro ist eine persönliche Seite, deren Inhalt in meiner alleinigen Verantwortung liegt. Der Text ist unter der CreativeCommons-Lizenz (BY-NC-SA) verfügbar. Weitere Informationen auf die Nutzungsbedingungen und dem Autor.
Referenzen
Diese Verweise und Links verweisen auf Dokumente, die während des Schreibens dieser Seite konsultiert wurden, oder die zusätzliche Informationen liefern können, aber die Autoren dieser Quellen können nicht für den Inhalt dieser Seite verantwortlich gemacht werden.
Der Autor dieser Website ist allein dafür verantwortlich, wie die verschiedenen Konzepte und Freiheiten, die mit den Nachschlagewerken gemacht werden, hier dargestellt werden. Denken Sie daran, dass Sie mehrere Quellinformationen austauschen müssen, um das Risiko von Fehlern zu reduzieren.



