Graphes et arbres
Arbre
Un arbre est un graphe simplement connexe, non orienté, sans cycles (et donc forcément sans boucles1), dans lequel nous ne pouvons retrouver qu'une seule chaîne pour relier deux sommets distincts.
Le graphe d'un arbre comporte toujours exactement n-1 arêtes2.
Racine d'un graphe
La racine r dans le cas d'un graphe orienté est le sommet à partir duquel nous pouvons accéder à chaque autre sommet du graphe : ∀ y : M[r,y]=1. Ce sommet (racine) est dit ascendant à tout autre sommet.
Arborescence
Nous appelons arborescence un graphe orienté qui possède une racine et pour lequel nous avons pour chaque sommet un seul chemin depuis la racine.
Arbre et arborescence
Les concepts d'arbre et d'arborescence ne sont pas figés. Dans certains cas nous aurons besoin de passer d'une notion à l'autre.
Nous pouvons orienter un arbre à partir d'un sommet. Dans ce cas nous pouvons avoir une arborescence.
Nous pouvons considérer une arborescence comme un graphe non orienté, et dans ce cas nous avons un arbre.
Lorsque nous ne pouvons ajouter une arête ou un arc d'un graphe à un de ses sous-graphes sans perdre le caractère d'arbre ou d'arborescence, nous pouvons dire que le sous-graphe est un arbre maximal ou une arborescence maximale.
Forêt
Lorsque nous avons un graphe composé d'arbres, nous parlons de forêt. Comme un arbre peut généralement être décomposé en sous-arbres, nous avons généralement une forêt dès que nous avons un arbre dans notre graphe.
Exercice
Voici quelques graphes, à vous de déterminer si nous sommes en présence d'un arbre, d'une arborescence, d'une forêt...
| 
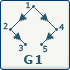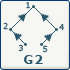| L'orientation de G2 ne nous permet pas de déterminer une racine.
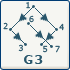| Par contre nous avons 2 arbres constituées par les sous graphes {1,2,3,4,5} et {6,7}
Par contre nous avons 2 arborescences constituées par les sous graphes {1,2,3,4,5} et {6,7}
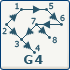| Nous sommes en présence d'un cycle.
Il existe par exemple plusieurs chemins depuis 2 vers 3
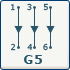| Par contre nous avons 3 arbres constituées par les sous graphes {1,2}, {3,4} et {5,6}
Par contre nous avons 3 arborescences constituées par les sous graphes {1,2}, {3,4} et {5,6}
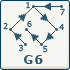| L'orientation de G6 ne nous permet pas de déterminer une racine.
Deutsche Übersetzung
Sie haben gebeten, diese Seite auf Deutsch zu besuchen. Momentan ist nur die Oberfläche übersetzt, aber noch nicht der gesamte Inhalt.Wenn Sie mir bei Übersetzungen helfen wollen, ist Ihr Beitrag willkommen. Alles, was Sie tun müssen, ist, sich auf der Website zu registrieren und mir eine Nachricht zu schicken, in der Sie gebeten werden, Sie der Gruppe der Übersetzer hinzuzufügen, die Ihnen die Möglichkeit gibt, die gewünschten Seiten zu übersetzen. Ein Link am Ende jeder übersetzten Seite zeigt an, dass Sie der Übersetzer sind und einen Link zu Ihrem Profil haben.
Vielen Dank im Voraus.
Dokument erstellt 22/11/2009, zuletzt geändert 09/03/2020
Quelle des gedruckten Dokuments:https://www.gaudry.be/de/graphes-arbres.html
Die Infobro ist eine persönliche Seite, deren Inhalt in meiner alleinigen Verantwortung liegt. Der Text ist unter der CreativeCommons-Lizenz (BY-NC-SA) verfügbar. Weitere Informationen auf die Nutzungsbedingungen und dem Autor.
Referenzen
Arbres : lien interne, Les arbres en programmation.
INFOB321 - Théorie des graphes : JP Leclercq, Cours de Théorie des Graphes et réseaux de Petri
(September 2008)
Diese Verweise und Links verweisen auf Dokumente, die während des Schreibens dieser Seite konsultiert wurden, oder die zusätzliche Informationen liefern können, aber die Autoren dieser Quellen können nicht für den Inhalt dieser Seite verantwortlich gemacht werden.
Der Autor Diese Website ist allein dafür verantwortlich, wie die verschiedenen Konzepte und Freiheiten, die mit den Nachschlagewerken gemacht werden, hier dargestellt werden. Denken Sie daran, dass Sie mehrere Quellinformationen austauschen müssen, um das Risiko von Fehlern zu reduzieren.
