Analyse relationnelle et cardinalité

Table des matières

Occurrences des relations

Un objet peut être décomposé en un nombre prédéfini ou indéfini d'occurrence, la représentation de ces occurrences formant une superposition de rectangles qui alourdissent le schéma. Il est possible de représenter autrement le nombre d'occurrence (de degré de participation des objets à une relation): la cardinalité.

Occurences et relations

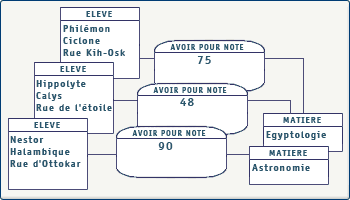
Analyse des relations

  • L'élève Nestor Halambique n'a pas participé aux tests, il n'est donc relié à aucune matière.
  • L'élève Philémon Ciclone a participé au test en égyptologie, mais pas à celui d'astronomie.
  • L'élève Hippolyte Calys a participé aux deux tests.
  • Un seul élève a participé au test en astronomie.
  • Deux élèves ont participé au test en égyptologie.

Remarque sur les occurrences des relations

Il est tout à fait possible que personne ne se présente à un test, ou que pour un type de matière il n'existe pas de test.

Table des matières Haut

Représentation des cardinalités

Cardinalités et relations

Cardinalités de la relation

Commençons par ceux situés du côté de l'objet élève:

  • Nous appellerons ces chiffres cardinalité de l'objet élève.
  • Le zéro est la borne inférieure, et signifie qu'un élève participe au minimum zéro fois à la relation (Nestor Halambique était absent lors des tests).
  • Deux est la borne supérieure, car Hyppolite Calys a participé à deux tests (en égyptologie et en astronomie).

Observons maintenant les chiffres placés à côté de l'objet matière:

  • Ces chiffres forment la cardinalité de l'objet matière.
  • Pourquoi zéro? Parce qu'il peut exister une matière qui ne soit pas cotée (voir remarque).
  • Le deux est justifié par le fait que l'égyptologie participe deux fois à la relation (Hippolyte Calys et Philémon Ciclone ont été testés sur cette matière).

Remarques sur le schéma de la relation

  • Dans le cas où la borne supérieure est indéterminée, nous remplacerons le chiffre par la lettre n.
  • Il est cependant préférable d'affecter un valeur précise aux bornes, car ces valeurs permettront une optimisation ultérieure du modèle.

Résumé sur les cardinalités des relations

  • Une valeur minimum à 0 signifie qu'au moins une occurrence de l'objet n'est pas liée à l'association.
  • Une valeur minimum à 1 signifie que toutes les occurrences de l'objet sont liées à l'association.
  • Une valeur maximum à 1 signifie qu'aucune occurrence de l'objet n'est liée plus d'une fois à l'association.
  • Une valeur maximum à n signifie qu'au moins une occurrence de l'objet est liée plusieurs fois à l'association.

A partir de ces valeurs minimum et maximum possibles, il existe quatre types de cardinalité :

  • (0,1) : une occurrence de l'objet n'est jamais liée plus d'une fois à l'association.
  • (1,1) : une occurrence de l'objet est toujours liée une et une seule fois à l'association.
  • (1,n) : une occurrence de l'objet est toujours liée au moins une fois à l'association.
  • (0,n) : aucune précision donnée.

Position des cardinalités

Dans les MCD de Merise (comme dans les schémas entité-association), la position de la représentation des cardinalités est inversée par rapport à celle en UML. Nous devons donc lire dans ce sens : nom de l'entité 1/nom de la relation/cardinalité qui se trouve près de l'entité 1/nom de l'entité 2.

Version en cache

21/11/2024 09:43:26 Cette version de la page est en cache (à la date du 21/11/2024 09:43:26) afin d'accélérer le traitement. Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la dernère version de la page.

Document créé le 19/03/2002, dernière modification le 26/10/2018
Source du document imprimé : https://www.gaudry.be/analyse-relationnelle-cardinalite.html

L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.